Các công thức nguyên hàm cơ bản, nâng cao đầy đủ nhất
Một công thức khá quan trọng, áp dụng nhiều trong quá trình làm bài tập đó chính là bảng công thức nguyên hàm mà theo Thao68 thấy rằng nó được áp dụng khá nhiều trong quá trình giải các bài toán. Chính vì thế, những bạn nào đang học lớp 12 nên tham khảo qua các công thức này để giải quyết các bài tập giải thích.
Với bài viết tổng hợp, các công thức nguyên hàm cơ bản, nâng cao đầy đủ các bạn có thể tham khảo và áp dụng để giải quyết các bài toàn trong quá trình học tập của mình nhé.
Contents
Định nghĩa nguyên hàm là gì?
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
- Kí hiệu: ∫ f(x)dx = F(x) + C.
Tham khảo các công thức đạo hàm lớp 11 nhất
Định lí 1:
1) Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.
Tính chất của nguyên hàm
• (∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
• Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
• ∫ kf(x)dx = k∫ f(x)dx với k là hằng số khác 0.
• ∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx.
Bảng các nguyên hàm cơ bản
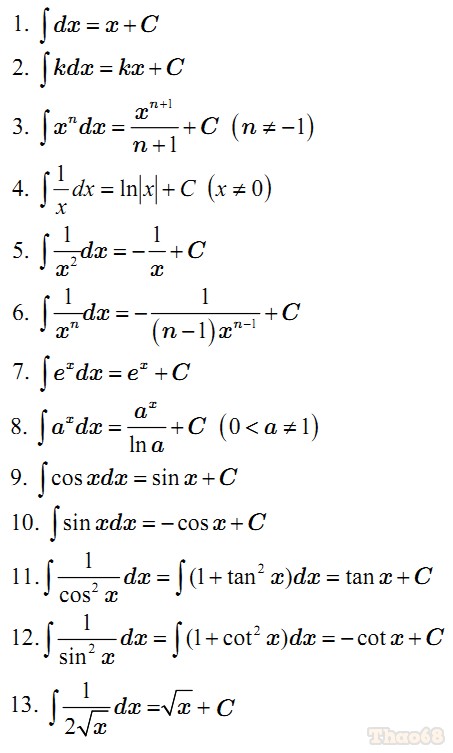
Chia sẻ những công thức lượng giác đầy đủ nhất cho các bạn
Bảng nguyên hàm mở rộng (a ≠ 0)
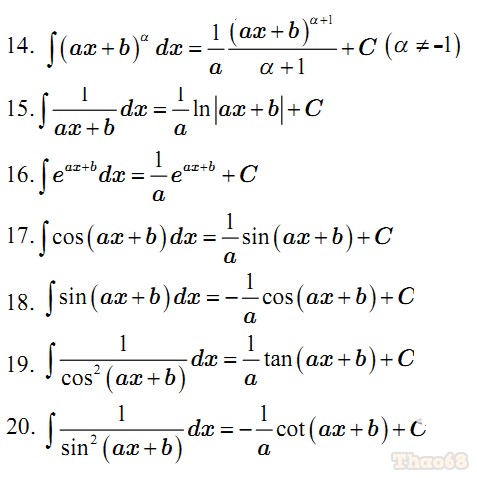
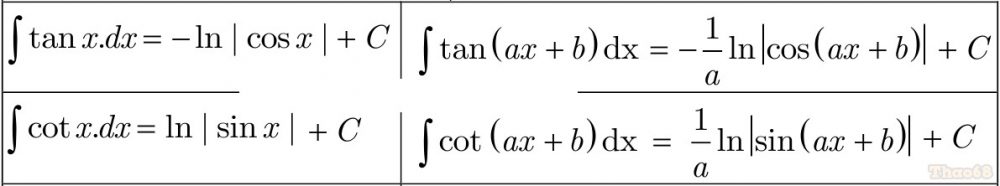
Nếu F(x) là một nguyên hàm của f(x) thì:
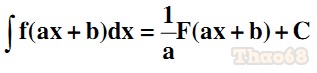
Bảng nguyên hàm nâng cao (a ≠ 0)

Với bài viết tổng hợp công thức nguyên hàm cơ bản, nâng cao đầy đủ Thao68 hy vọng rằng nó sẽ giúp các bạn học sinh lớp 12 giải quyết khá nhiều bài tập trung quá trình học của mình nhé!
Hỏi & đáp -Các công thức đạo hàm lớp 11 từ cơ bản, cấp cao đầy đủ
Tổng hợp các công thức lượng giác lớp 10 đầy đủ nhất
Thứ, ngày, tháng tiếng Anh với cách ĐỌC và HỌC chuẩn nhất
Danh sách biển số xe ở các tỉnh thành nước ta đầy đủ
Tên các nước trên thế giới và ý nghĩa các quốc gia
Tên các ngón tay và thứ tự các ngón tay chính xác nhất
Khối A00 gồm môn thi, ngành nghề và trường đại nào nào tổ chức thi?