Công thức tính diện tích và chu vi hình bình hành đầy đủ nhất

Trong các kiến thức toán học, thì công thức tính diện tích và chu vi hình bình hành được xem là kiến thức phổ thông, buộc các bạn phải nhớ nhằm vận dụng vào để giải quyết các bài tập. Không những thế, các công thức này còn được áp dụng khá nhiều trong cuộc sống sau này.

Và với bài viết này của Thao68, các bạn có thể ôn lại các công thức tính diện tích, chu vi hình bình hành nếu như các bạn lỡ có quên cực kỳ hiệu quả đấy nhé!

Contents

Hình bình hành là gì?

Hình bình hành là một tứ giác, có các cặp cạnh đối song song và bằng nhau. Nó được xem là một trường hợp đặc biệt của hình thang trong toán học.

Dấu hiệu nhận biết hình bình hành:

Công thức tính diện tích chu vi hình thoi đầy đủ nhất

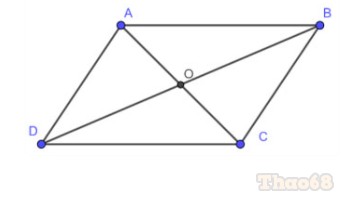
Công thức tính diện tích hình bình hành

Ta có: Diện tích hình bình hành bằng độ dài cạnh đáy nhân với độ dài chiều cao

Trong đó: B = độ dài cạnh đáy, H = độ dài chiều cao và S là diện tích.

Công thức S:

Công thức tính chu vi hình bình hành

Ta có: Chu vi của một hình bình hành bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.

Công thức:

Tham khảo: Công thức tính chu vi hình tròn cho các bạn học sinh

Ví dụ: Cho một hình bình hành ABCD với hai cạnh a và b lần lượt và 5cm và 7 cm. Vậy chi vi của hình bình hành ABCD bằng bao nhiêu?

Áp dụng công thức trên ta có chu vi hình bình hành: C = (a +b) x 2 = (7 + 5) x 2 =12 x 2 = 24 cm

Qua bài viết ở trên, mọi người có thể ôn lại kiến thức toán học về diện tích, chu vi hình bình hành để áp dụng giải quyết các bài tập và vận dụng vào trong cuộc sống một cách hiệu quả nhất nhé!

Hỏi & đáp -